응애맘마조
YawPitchRoll, 짐벌락, 쿼터니언 본문
주의 : 해당 게시물에서 작성될 내용은 과제를 해결하기 위해 출처의 내용을 그대로 작성한 부분이 많으며 일절 광고나 수익 창출 목적으로 쓰인 것이 아님을 밝힙니다.
YawPitchRoll은 XYZ 축을 중심으로 회전하는 것을 말합니다.
Roll은 X축을 중심으로 회전합니다.
Pitch는 Y축을 중심으로 회전합니다.
Yaw는 Z축을 중심으로 회전합니다.
전의 과제로 만들었던 걷는 모션의 영상으로 확인하면
짐벌락에 대해서 먼저 설명하기 전에 짐벌에 대해서 알아야 합니다.
먼저 짐벌은 물체가 회전하도록 중심축을 가진 구조물입니다. 3차원 공간에 놓인 강체의 방향은 오일러 각도를 사용하여 세 번의 회전을 통해 얻을 수 있습니다.
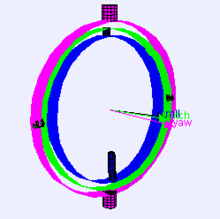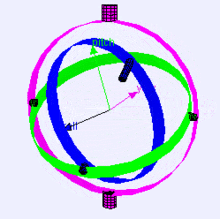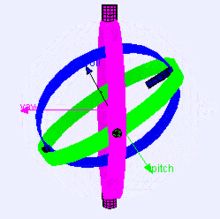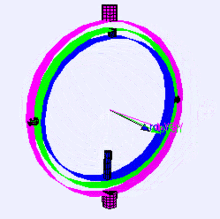
오일러 각도는 강체가 놓인 3차원 공간에 표시하기 위해 도입한 세 개의 각도이며 위에서 말한 YawPitchRoll입니다.
(강체는 외부의 힘에 의해 변하지 않는 물체를 말합니다.)
그럼 짐벌락이라는 것은 위에서 말한 오일러 각도를 이용해서 두 개나 세 개의 축이 겹쳐서 한 개나 두 개의 축이 자유도를 잃어서 같은 방향으로 회전축이 겹치는 현상을 말하며 이렇게 되면 원하는 방향으로 회전이 불가능합니다. 발생하는 이유는 회전의 연산을 각 축의 성분으로 나눠서 계산하기 때문입니다. 위의 이미지에서도 축이 겹치는 현상이 나오는 것이 짐벌락입니다.
이러한 짐벌락 현상을 해결하기 위한 것이 쿼터니언이고 사원수라고도 합니다. 쿼터니언은 x, y, z, w의 4개의 실수로 와 허수 i, j, k로 구성되어 있습니다. 각각의 값은 x, y, z, 벡터와 스칼라입니다. 모든 축을 한 번에 계산할 수 있기 때문에 짐벌락 문제가 생기지 않고 방향과 회전을 모두 표현할 수 있습니다. 네 개의 실수 성분을 가지고 덧셈과 곱셈의 결합법칙 및 덧셈의 교환법칙은 만족시키지만 곱셈의 교환법칙은 성립되지 않습니다.
이외의 쿼터니언은 너무 방대해서 나중에 강의나 과제에서 작성하겠습니다.
읽어주셔서 감사합니다.
